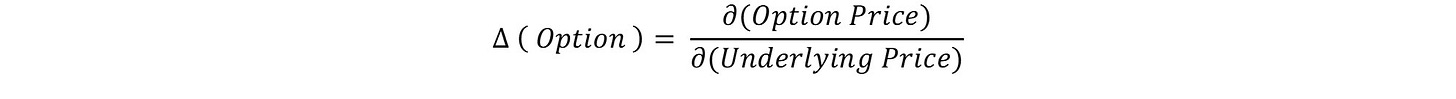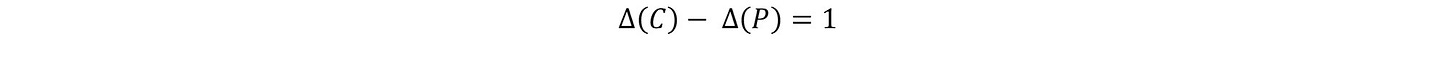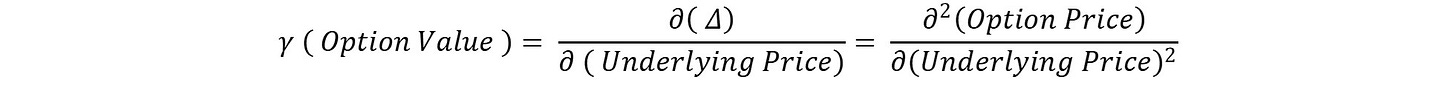Option Delta and Gamma
The price of options can be determined by various models like Black-Scholes Model, Binomial Pricing Model, Monte-Carlo Simulation Model etc. These models often incorporate the price and volatility of the underlying to establish the basis of calculating the current price of the option. Although these factors are very important, they are not the sole determinants of how the option price will behave. The price of an option is affected by various factors. These factors are most popularly expressed in terms of Greek symbols and are hence called Option Greeks.
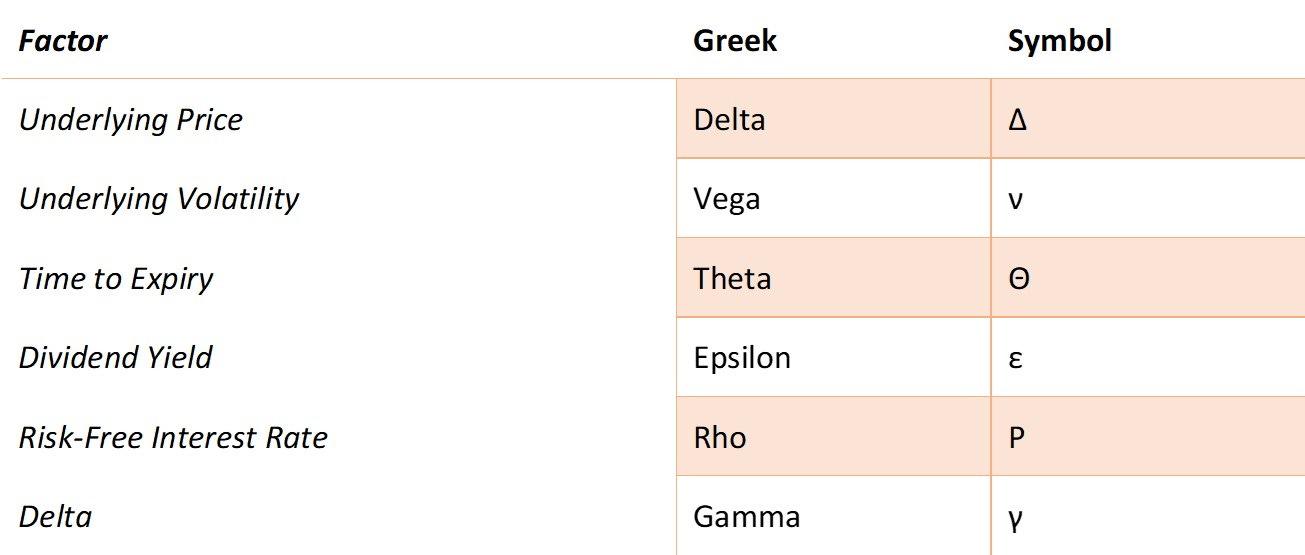
The greeks that will be discussed include:
All of the above greeks except gamma are first-order greeks, i.e., they are first-order derivatives of the option price over the respective factors, i.e., change in option price due to change in factor. Gamma is the second order derivative of delta, i.e., a derivative of Delta over price, i.e., change in delta due to change in price.
Option Delta ( Δ )
Option Delta is probably the most commonly used Greek. It measures the change in price of the option due to the change in the price of the underlying.
The value of delta is always between -1 and +1. A delta of 0.30 means that if the share price increases by Rs. 1, the value of the option will increase by 0.30 and vice versa. Long Calls always have delta greater than or equal to 0 because long calls always benefit from an increase in underlying price. Similarly, Short Puts also have a positive delta because they benefit from increasing share price. In a similar manner, Long Puts and Short Calls have delta between -1 and 0 because they benefit from decreasing share prices. The delta of the underlying is always equal to 1 because delta measures change in price w.r.t change in underlying price.
It should also be noted that delta has a linear combination. That means that if a portfolio contains calls, puts and the underlying , the total delta of the portfolio is simply the total delta of calls, puts and the underlying combined.
Using all the information given above along with put-call parity, the relationship between the delta of calls and puts can be established. Since the strike price of an option remains constant, the delta of the strike price is 0. By Put-Call Parity we know that a Long Call and Short Put have an equal Payoff as a Forward, which has a delta equal to 1.
As a result,
Options are often quoted in terms of delta like 30delta Call, 50delta Put, etc. The delta is quoted in absolute terms and the sign associated with the type of option is assumed to be implicit since calls only have positive delta and puts only negative. Delta is thus used to represent the number of shares that the options contract is equal to. For example., A 30delta call options contract which includes 100 call options has a total delta of +30, which is equal to holding a portfolio of 30 stocks of the underlying, since it has a delta of 1. Similarly, an 80delta Put Contract will have a delta of -80 which is equal to shorting a portfolio that contains 80 stocks of the underlying.
The absolute value of delta of an option is also often understood as the moneyness of the option, i.e., the probability of an option expiring ITM, thus it is believed that a 15delta call has a 15% chance of expiring in the money.
Taking into consideration the delta is very important when adding options to a portfolio of the underlying security. Since the delta of the underlying is always 1, traders and investors often use delta-hedging techniques to reduce the risk of their portfolios. Consider a situation where an investor is long 150 stocks. The delta of the portfolio is +150. In order to hedge the position, the investor may purchase 3 50delta Put contracts of 100 options each which has a total delta of { 100 x 3 x (-0.50)} = -150. Thus, the portfolio is hedged in terms of volatility of returns due to changes in price of the underlying. But, buying put options can be expensive. The investor also has the option of selling 2 Call options contracts of say 25Delta Calls which will have a total delta of -50 and using the funds from that to buy 2 50delta Put Option contracts having a total delta of -100 leading to a total delta of -150 for the options portfolio and completely hedging the return of the underlying portfolio. This was just an example of using a combination of options contracts to completely hedge the returns of the stock portfolio. There can be numerous combinations of both puts and calls of different deltas that can be used to either completely or partially hedge the returns of the stock portfolio.
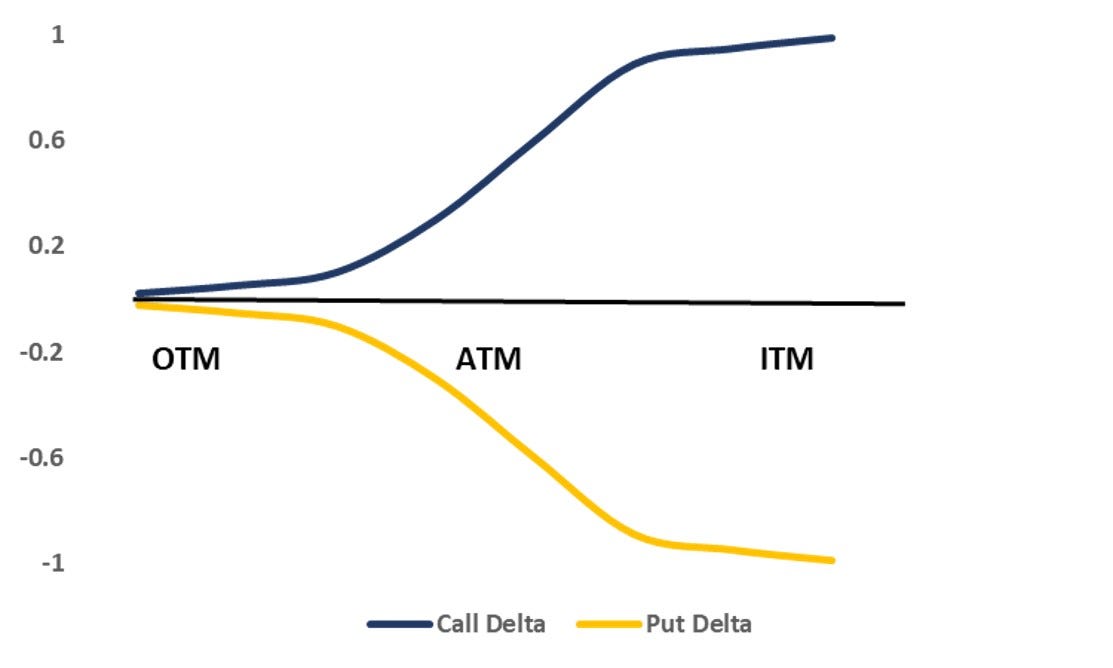
It should be noted however that the delta of a particular options contract is constantly changing. The delta of an options is highest in absolute terms when it is deep in the money. It decreases as the underlying price moves towards the strike. When the option is at the money, the delta is close to 0.50 in absolute terms and as the option moves out the money, the delta falls and ultimately becomes close to 0 when the option is deep in the money. The reason for this can be understood from various perspectives. Consider a Call option on XYZ at a strike price of 200 expiring after 3 months. If the current price of XYZ is 350, the call is deep in the money. It is highly possible that the call will expire in the money and will pay 150. When options are deep in the money, holding the long option is almost equal to going long the underlying itself, and as a result, the change in option price is almost equal to the change in the underlying price and hence the delta is almost equal to 1. As the underlying price falls, it starts becoming less probable that the option will expire in the money, and so holding the option becomes less lucrative and the option starts behaving less and less like the stock and the delta falls, i.e., for change of 1 in the option price, the option changes by only .70. When the underlying price approaches the strike price, the investor is unsure whether the option will expire in the money or out of the money and as a result, the delta nears 0.50. as the price continues to fall, the probability continues to decline and almost becomes 0 when the option becomes OTM.
Thus, delta hedged positions are constantly changing. It is not necessary that a position that had a net delta of 0 today when the markets opened will have a net delta of 0 when the markets close. The portfolio has to be continuously hedged and this is one of the problems with delta-hedging the portfolio. Another problem with delta-hedging the portfolio is that delta is only effective in small changes over small amounts of time. In case of big changes over long periods of time, it becomes ineffective because it does not incorporate the convexity of the change in value.
In addition to this, the rate at which delta changes is also not linear. It changes by varying amounts. The change in delta w.r.t the change in underlying is called the Option Gamma.
Option Gamma ( γ )
Gamma is the second order derivative of change in option value w.r.t change in price, or it is the change of change in value w.r.t. change in price, i.e., change in value of delta w.r.t. change in price.
The value of Gamma lies between 0 and 1 and is always positive for long options and negative for short options. For long calls, as the underlying price increases, the delta moves towards 1 from 0 and hence increases. If the stock price decreases, the call becomes less attractive and its delta will fall leading to fall in gamma. Thus, the call delta rises with increase in stock price and falls with decrease in stock price. For long puts, as stock price increases, the put delta moves from -1 to 0, and hence increases in absolute terms. In a similar way, as the stock price falls, the delta moves from 0 towards -1 and the delta decreases as it becomes more negative. Thus, a long gamma position involves a case where the option delta increases with increase in stock price and falls with a fall in stock price. As the stock price increases, the short call becomes less and less profitable for the seller and has decreasing delta, whereas a short put becomes more profitable as the options becomes more likely to expire out of the money which is favorable to the option seller. In a similar way, when stock price falls, the short calls become more profitable and their delta increases whereas short puts become less profitable and their delta falls. Thus, in case of short options, as the share price increases, the delta falls and as share price falls, the delta increases leading to negative gamma.
When stock price increases, gamma is added to delta. Similarly, it is deducted from delta when stock price falls. Thus, delta of long gamma/positive gamma positions changes in the direction of the stock price whereas the delta of short gamma/negative gamma positions changes in opposite direction of stock price. So, gamma can be thought of a factor that magnifies the situation. It makes a good situation better and a bad situation worse.
Gamma incorporates the effect of convexity in delta-hedging the portfolio. It also shows the volatility of the option delta in a way. An option with a higher gamma will see higher changes in delta for unit change in the underlying. It is important to understand the consequences of this in the way the positions behave when price of the underlying changes. Gamma can cause changes in the option delta which will ultimately lead to a seemingly delta-neutral position attain delta-exposure and hence cause potential losses if left unchecked.
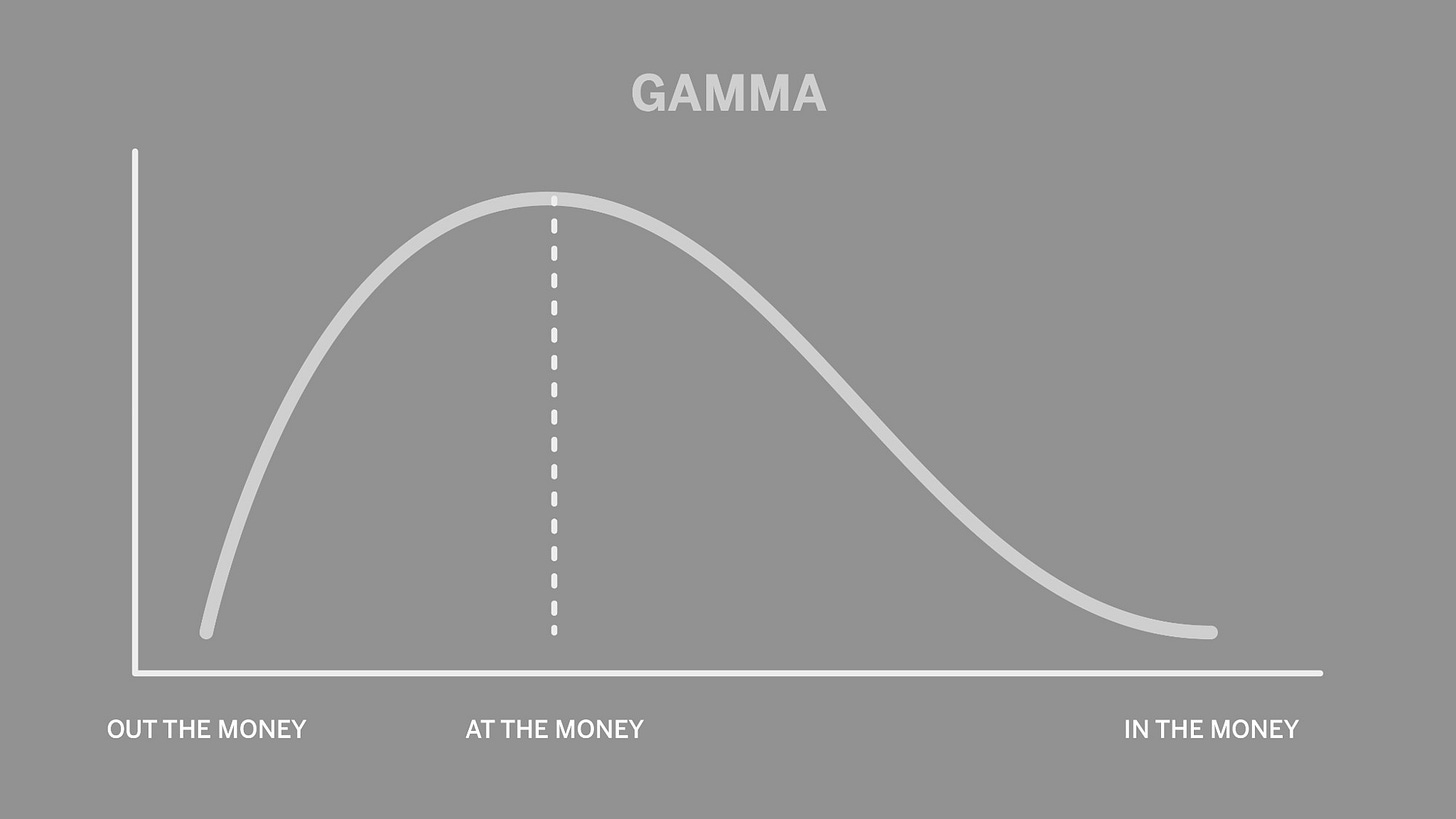
The gamma of an option has a highest value of around 0.5 when the option is ATM and nearing expiry. This is because when the option is ATM, the delta of the option is 0.5 which is often interpreted as a 50-50 chance between the option expiring in the money and out of the money. As a result, the delta of the option becomes very volatile because in one moment it might favour the option buyer and in one moment it might favour the option seller since it is so close to the strike price. This volatility was also visible in the graph of Delta which starts off flat, then becomes very steep when the option is ATM and then again becomes flat when the option is ITM. From this, it can also be understood that the Gamma of OTM and ITM options is also very low. This is because when an option is either fairly OTM or ITM, it is expected that it will expire OTM or ITM respectively and so there is less change in option premium for small changes in underlying price, leading to smaller changes in delta, leading to low values of gamma. For example, when option is deep OTM, the delta value is already very low, say 0.03 or such. In such a case, if the stock further falls, the delta has very little room to fall to, so gamma value is very low. In a similar manner, when option is deep ITM, the delta value is already very high, say, .85. in such a case, the delta has less room to increase further, so the changes are small leading to low values of gamma. In addition to the moneyness of options, the time left to expire also has an effect on gamma values. If expiry is near, ATM options have more volatile delta than options which have longer expiry leading to a higher value of gamma than options simply because of the higher amount of uncertainty that the option will expire ITM or OTM.
Like option Delta, option Gamma is also linearly combined to obtain a hedged position but hedging gamma is not easy for small retail traders.